Hot carrier photocurrent induced by 0.92 eV photon energy radiation in a Si solar cell

1. Laboratory of Electronic Processes, Center for Physical Sciences and Technology, Saulėtekio Ave. 3, LT-10257 Vilnius, Lithuania
2. Department of Physics, Vilnius Gediminas Technical University, Saulėtekio Ave. 11, LT-10223 Vilnius, Lithuania

Abstract

Absorption of the below-bandgap solar radiation and direct pre-thermalizational impact of a hot carrier (HC) on the operation of a single-junction solar cell are ignored by the Shockley-Queisser theory. The detrimental effect of the HC is generally accepted only via the thermalization-caused heating of the lattice. Here, the authors demonstrate experimental evidence of the HC photocurrent induced by the below-bandgap 0.92 eV photon energy radiation in an industrial silicon solar cell. The carriers are heated both through direct free-carrier absorption and by residual photon energy remaining after the electron-hole pair generation. The polarity of the HC photocurrent opposes that of the conventional generation photocurrent, indicating that the total current across the p-n junction is contingent upon the interplay between these two currents. A model of current-voltage characteristics analysis allowing us to obtain a reasonable value of the HC temperature was also proposed. This work is remarkable in two ways: first, it contributes to an understanding of HC phenomena in photovoltaic devices, and second, it prompts discussion of the HC photocurrent as a new intrinsic loss mechanism in solar cells.

Introduction

The only efficient optical process that generates electron-hole pairs necessary for the operation of a solar cell is the absorption of solar photons with energy equal to a semiconductor forbidden energy gap 𝐸_𝑔 [Fig. 1a), process 1]. The Shockley-Queisser theory, which predicts the maximum possible solar cell efficiency, states that photons having energy lower than the bandgap are not absorbed at all [Fig. 1(b), long wavelength range from 𝐸_𝑔[1]. This optical waste is called “below-bandgap loss” [2]. Absorption of photons with energy above the bandgap creates electron-hole pairs with excess energy. As a rule, the residual photon energy is not only unused for carrier generation, but also undesirably heats the crystal lattice, resulting in reduced efficiency of the solar cell. This waste process is called “thermalization loss” because the carriers dissipate their excess energy via carrier-carrier and carrier-phonon interactions, i.e., they thermalize [3].

In general, carriers with energy exceeding equilibrium are called hot carriers (HCs). HCs can be created by both the below- and above-bandgap photons [Fig. 1(b), entire oblique-lined zone below the red line] [4]. In the first case, the carriers are heated by the intraband absorption of light [5]. Although the free-carrier absorption coefficient is much lower than the interband absorption coefficient [6], the presence of such carrier heating and the formation of a HC (pre-thermalized carrier) electrical signal have been evidenced in semiconductor structures. For instance, HCs have found application in microwave [7, 8] and terahertz [9] radiation detection. CO2 laser light (photon energy of 0.117 eV) induced HC photocurrent across Si [10], Ge [11], and GaAs p-n diodes [12] [Fig. 1(a), process 2]. Typical properties of the photocurrent are its polarity, which indicates carrier flow up the barrier, linear dependence on excitation power, and fast response to laser light pulses. The response time of the HC effect is fundamentally defined by the carrier energy relaxation time, which is of the picosecond order [3, 6].

‌

Direct experimental evidence of HCs in conventional single-junction solar cells exposed to the above-bandgap radiation is not announced widely. The presence of HCs has been shown indirectly. A small increase in the open-circuit voltage was attributed to the extraction of hot electrons generated near the collector [13]. Simulation of selective energy contact solar cells showed the possibility of enhanced cell efficiency by collecting hot electrons within a special range of energies onto external electrodes [14]. HC energy harvesting was considered by impact ionization [15], the use of nanowires [16], or optical extraction using rare-earth dopants [17]. An efficient solar cell based entirely on the HC phenomenon was presented in Ref. 18. Its successful operation is possible through a marked reduction in the thermalization rate [19, 20]. However, the numerous theoretical and experimental investigations devoted to the development of HC solar cells (see Refs. 21–24 and references therein), have so far not led to practically applicable HC solar cells.

Despite the large difference in the interband and intraband absorption coefficient values, the simultaneous coexistence of the HC and generation photocurrents has been demonstrated. The HC photocurrent started manifest-ing itself [Fig. 1(a), process 3] at high excitation intensity when the generation photocurrent was already saturated in the narrow-gap HgCdTe [25] and InSb [26] p-n diodes. Competition between the HC photocurrent and the two-photon absorption-caused generation current has been advertised in GaAs p-n diodes irradiated with a 1.064 μm long laser radiation [27]. Here, the generation photocurrent arose against the HC one because of its stronger (square) dependence on light intensity. Note that in any case, the HC photocurrent flows in the direction opposite to the carrier generation-caused photocurrent, which, in turn, benefits the operation of the solar cell.

Thus, the contribution of HCs to photovoltaics remains ambiguous. On one hand, the classical Shockley-Queisser theory ignores carrier heating by the below-bandgap photons and the direct pre-thermalizational effect of HCs on solar cell efficiency. On the other hand, HCs serve as a driving force for the search for modern photovoltaic devices such as HC solar cells or infrared detectors [28].

In this work, the authors explore the peculiarities of HC phenomena in solar cells. The HC photocurrent induced by radiation close to but below the bandgap (0.92 eV vs. 1.1 eV) radiation in an industrial silicon solar cell is investigated. The wavelength is chosen to avoid single-photon generation of electron-hole pairs which could suppress the heating of carriers. In addition, to reveal the inevitable presence of the HC photocurrent, the authors also use the above-bandgap (1.17 eV vs. 1.1 eV) laser radiation. The peculiarities of the HC photocurrent are investigated by a comparative analysis of the two photocurrents, HC and generation, in their current-voltage (I-V) and current-power dependencies. The carrier temperature is evaluated using a novel method based on the temperature coefficient of the I-V characteristics.

Experiment

Industrial polycrystalline silicon solar cells (SoliTek, Vilnius, Lithuania) were used for the investigation. Carrier densities were n ≈ 1020 cm^-3 and p ≈ 1016 cm^-3 in the emitter and base, respectively. The cells were cut into 2 × 2 mm2 samples. To avoid the formation of a photo response across the metal contacts, these were situated on the edge of the sample. A passively Q-switched Nd:YVO4 oscillator with a 4-pass amplifier emitting a wavelength of 1.342 μm served as a light source. Its photon energy of 0.92 eV was close to but less than a poly-crystalline silicon bandgap of 1.1 eV. Laser pulses with a duration of 1.7 ns, a repetition rate of 50 Hz, and a light intensity ranging from 0.06 to 0.36 MW/cm² were used for excitation. The intensity was varied by adjusting the laser pump power. Pulsed laser radiation of 1.064 μm wavelength (17 ns long pulses, 50 Hz) was used for a comparative analysis. Nanosecond-long excitation pulses are a convenient tool for recognizing the fast HC effect. Measurements were performed in the photocurrent regime (Fig. 2). A load resistor of 50 Ohms enabled matching of the circuit impedance and obtaining proper time-dependent characteristics of the photo response. To provide the measurements with the bias voltage and to minimize the electronic noise, a handmade DC voltage source (0–9 V and 0–0.3 A) was used. In general, the photo response consisted of two components with opposite polarities (schematically, typical photo response is depicted on the oscilloscope screen in Fig. 2). The photocurrent transients and peak value of each sub pulse were fixed and measured using an Agilent Technologies DSO6102A digital oscillo-scope with registration accuracy: vertical (voltage) ± 2.0% of full scale, horizontal (time) ± 0.0015% with a resolution of 2.5 ps.

‌

Results and discussion

Pulsed laser radiation induces a photocurrent composed of two components with opposite polarities, as mentioned above. The I-V characteristics of the dark and illuminated sample built using individual peak values of each photo-current component and considering their corresponding direction are shown in Fig. 3 as solid lines. At the used 0.36 MW/cm² laser light intensity, the values of both short-circuit photocurrent components are almost the same, while the forward bias voltage strongly changes their ratio to the disadvantage of the “blue” one.

‌

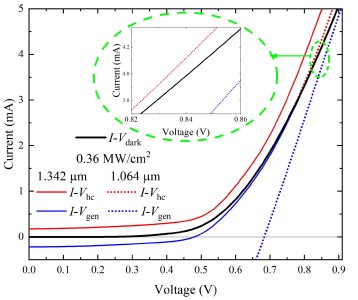
Concerning the origin of the photocurrent components, the direction and fast course of the first sub pulse (see inset in Fig. 4) indicates that it can be attributed to the HC photocurrent 𝐼 _hc [29]. Process 2 of Fig. 1(a) schematically explains the formation of the HC photocurrent: a free electron is heated by a below-bandgap photon and diffuses across the junction during the step-like thermalization. The diffusion is driven by the carrier density gradient, and the high electron energy should be enough to overcome the potential barrier of the junction. Note that this photocurrent direction coincides with the forward current across the junction. Another photocurrent sub pulse of opposite polarity is obviously caused by the electron-hole pair generation 𝐼_gen [blue arrows in Fig. 1(a)]; its slow run is defined by the carrier lifetime. To distinguish one photocurrent component from another, the HC component is represented in red, and the generation-attributed one is depicted in blue.

‌

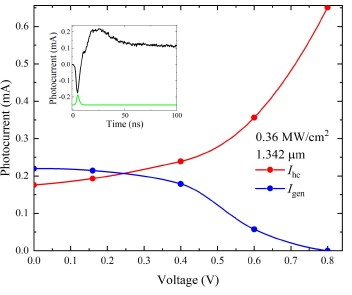
It is noteworthy that, in contrast to the generation current (Fig. 3, blue dotted line), no HC short-circuit photocurrent is detected under the illumination of a 1.064 μm long laser radiation (photon energy is above the bandgap). Nevertheless, the HC photocurrent starts manifesting itself at a forward bias exceeding ~ 0.8 V (Fig. 3, red dotted line in the top right corner in the inset). The peak values of the photocurrent sub pulses vs. the applied voltage are depicted in Fig. 4. The sharp rise of the HC photocurrent 𝐼_hc above 0.5 V bias is worth noting. Similar boosts have been detected by other authors [1, 30]. Such rise means that the HCs reach favourable conditions to flow across the junction at a particular bias, which is most probably related to the reduced potential barrier height of the junction.

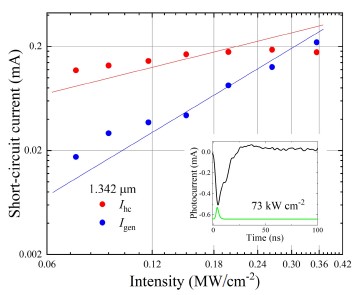
As Fig. 5 shows, the generation photocurrent follows a close to square law in its dependence on excitation intensity. Such a relationship reflects a two-photon absorption [29, 31]. If the HC photocurrent is defined purely by the intraband absorption, it should follow the linear law, as was seen in the case of photon energy much lower than the semiconductor bandgap [12]. The sublinear dependence of 𝐼_hc in this study has a three-fold back-ground. First, the increase in the two-photon absorption coefficient value with increasing excitation power leaves fewer photons for free-carrier absorption. Second, the residual single-photon energy left over after the generation and used for free-carrier heating is much lower: (2ℎν – 𝐸_𝑔÷2 = 0.365 eV as compared to ℎν = 0.92 eV. Third, the generation photocurrent component oppresses the HC one of opposite polarity because it grows twice as fast with excitation intensity.

‌

A diode I-V characteristic depends on temperature. Its shift can be described by the temperature coefficient, which indicates the change in voltage per degree of temperature at a fixed current value [32]

\( \left.\alpha_T=\frac{\Delta U}{\Delta T} \right\rvert\, I=\text { const } \mid \) (1)

Here, Δ𝑈 is the voltage change, and Δ𝑇 is the corresponding change in temperature. The dark I-V characteristics measured at room (𝑇= 300 K) and liquid nitrogen (𝑇= 80 K) temperatures are shown in Fig. 6. Taking 𝑈₃₀₀= 0.525 V and 𝑈₈₀= 0.958 V at a fixed current value of 0.238 mA, 𝛼_𝑇= −1.97 mV/K is obtained. This result falls well within the 1.855 to 2.19 mV/K range of the announced coefficient values for silicon solar cells [33–35]. On the other hand, the same 0.238 mA current flows in the illuminated case at room temperature. Now, the only difference between the two currents, the dark current and the photocurrent, which are equal in magnitude, is the carrier temperature. Taking corresponding voltages 𝑈_dark=𝑈₃₀₀=  0.525 V and 𝑈_ill= 0.250 V (see Fig. 6) and using the calculated 𝛼_𝑇 value, a difference between the carrier and lattice temperatures is obtained as follows:

\( \Delta T=\frac{U_{\text {ill }}-U_{\text {dark }}}{\alpha_T}|I=0.238 \mathrm{~mA}|=140 \mathrm{~K} \) (2)

The 0.238 mA magnitude of the current is chosen assum-ing that the dark current is weak enough at 𝑈_ill= 0.250 V, and the net current is defined only by the photocurrent (see Fig. 6). The proposed model of carrier temperature evalua-tion is supported by the following serial considerations: an increased excitation intensity will amplify the photo-current; the “illuminated” I-V characteristic will be shifted up; the voltage difference Δ𝑈 at fixed current will be higher, and as a result, the carrier temperature will be higher according to (2). Comparison of the obtained HC temperature with the results of other authors is uncertain because different experiments use different techniques under different conditions. Optical investigations, as a rule, heat the carriers using the above-bandgap laser radiation. For example, high-intensity (TW/cm²) femtosecond-long laser pulses were used in numerical pump-probe simulations, and electron temperatures over 4600 K in silicon were evaluated [36]. Fitting of the time-resolved luminescence spectra of bulk GaAs showed the dependence of the carrier temperature on the excitation level and delay time: the temperature varied from 1200 K to 300 K at a delay time of 1 ps to 100 ps, respectively [37]. Thus, the result of 440 K carrier temperature obtained under 0.36 MW/cm²-intense below-bandgap radiation of nanosecond-long laser pulses seems reasonable. It is important to highlight that the suggested model provides a preliminary assessment of the HC temperature, which is expected to be relatively independent of the selected constant current value because the I-V curves at 𝑇= 300 K and 𝑇= 80 K are almost parallel, and the voltage difference 𝑈_ill− 𝑈_dark, as used in (2), remains nearly the same.

Conclusions

In conclusion, the below-bandgap radiation of a 1.342 μm wavelength causes free-carrier heating in silicon and induces a HC photocurrent across the Si p-n junction. In contrast to the electron-hole generation-induced current, the HC photocurrent has favourable conditions for flow at the forward bias voltage. Increasing radiation intensity suppresses the HC photocurrent because of the increasing role of the two-photon absorption and the corresponding rise in the generation photocurrent. The proposed method of the temperature dependence analysis of the current-voltage characteristics allows obtaining reasonable values of the HC temperature. Concerning solar photovoltaics, several points are worth noting:

• The presence of the HC photocurrent has an adverse impact on the operation of a single-junction solar cell.
• The maximum power point of the cell is within the region of the forward bias, which is advantageous for the flow of the HC photocurrent.
• The HC photocurrent is induced by both above-bandgap and below-bandgap radiation. Although this work analyses single wavelength and high, much higher than the sunlight, radiation intensity-caused HC effect, there would still be a certain impact of the HCs if the whole solar spectrum were considered (some theoretical contemplations on this issue are presented in Ref. 4).
• The pre-thermalizational effect of the HC should be admitted as a new intrinsic fundamental loss (“pre-thermalization loss”) that opposes the approach of the realized solar cell efficiency to the theoretically predicted one. This work may serve as a call to the photovoltaic community to reconsider the Shockley-Queisser limit by incorporating the detrimental effect of the HCs.

References

1. ‌Shockley, W. & Queisser, H. J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519 (1961). https://doi.org/10.1063/1.1736034

2. ‌Hirst, L. C. & Ekins-Daukes, N. J. Fundamental losses in solar cells. Prog. Photovolt. Res. Appl. 19, 286–293 (2011). https://doi.org/10.1002/pip.1024

3. ‌Zhang, Y. et al. A review on thermalization mechanisms and prospect absorber materials for the hot carrier solar cells. Sol. Energy Mater. Sol. Cells 225, 1–13 (2021). https://doi.org/10.1016/j.solmat.2021.111073

4. ‌Masalskyi, O. & Gradauskas, J. Pre-themalizational effect of hot carriers on photovoltage formation in a solar cell. Ukr. J. Phys. Opt. 23, 117–125 (2022). https://doi.org/10.3116/16091833/23/3/117/2022

5. ‌Schroder, D. K., Thomas, R. N. & Swartz, J. C. Free carrier absorption in silicon. IEEE J. Solid-State Circuits 13, 180–187 (1978). https://doi.org/10.1109/JSSC.1978.1051012

6. ‌Dargys, A. & Kundrotas, J. Physical data for gallium arsenide. Handbook on Physical Properties of Ge, Si, GaAs, and InP (Science and Encyclopedia, Vilnius, 1994).

7. ‌Ašmontas, S. & Sužiedelis, A. New microwave detector. J. Infrared Millim. Terahrtz Waves 15, 525–538 (1994). https://doi.org/10.1007/BF02096235

8. ‌Anbinderis, M. et al. Microwave Detection Characteristics of Gated Asymmetrical Selectively Doped Semiconductor Structures at the Power and Frequency Variation. in 2nd IEEE Ukrainian Microwave Week (UkrMW) 79–83 (IEEE, 2022). https://doi.org/10.1109/UkrMW58013.2022.10037063

9. ‌Zabudsky, V., Dobrovolsky, V. & Momot, N. Detection of terahertz and sub-terahertz wave radiation based on hot-carrier effect in narrow-gap Hg1−xCdxTe. Opto-Electron. Rev. 18, 300–304 (2010). https://doi.org/10.2478/s11772-010-1026-7

10. ‌Encinas-Sanz, F. & Guerra, J. M. Laser-induced hot carrier photovoltaic effects in semiconductor junctions. Prog. Quantum Electron. 27, 267–194 (2003). https://doi.org/10.1016/S0079-6727(03)00002-8

11. ‌Umeno, M., Sugito, Y., Jimbo, T., Hattori, H. & Amenixa, Y. Hot photo-carrier and hot electron effects in p-n junctions. Solid-State Electron. 21, 191–195 (1978). https://doi.org/10.1016/0038-1101(78)90137-5

12. ‌Ašmontas, S., Gradauskas, J., Seliuta, D. & Širmulis, E. Photoelectrical properties of nonuniform semiconductor under infrared laser radiation. Proc. SPIE 4423, Nonresonant Laser-Matter Interaction (NLMI-10) (2001). https://doi.org/10.1117/12.431223

13. ‌Kempa, K. et al. Hot electron effect in nanoscopically thin photovoltaic junctions. Appl. Phys. Lett. 95, 1–3 (2009). https://doi.org/10.1063/1.3267144

14. ‌Shayan, S., Matloub, S. & Rostami, A. Efficiency enhancement in a single bandgap silicon solar cell considering hot-carrier extraction using selective energy contacts. Opt. Express 29, 5068–5080 (2021). https://doi.org/10.1364/OE.416932

15. ‌Kolodinski, S., Werner, J. H., Wittchen, Th. & Queisser H. J. Quantum efficiencies exceeding unity due to impact ionization in silicon solar cells. Appl. Phys. Lett. 63, 2405–2407 (1993). https://doi.org/10.1063/1.110489

16. ‌Fast, J., Aeberhard, U., Bremner, S. P. & Linke, H. Hot-carrier optoelectronic devices based on semiconductor nanowires. Appl. Phys. Rev. 8, 1–23 (2021). https://doi.org/10.1063/5.0038263

17. ‌Saeed, S., de Jong, E., Dohnalova, K. & Gregorkiewicz, T. Efficient optical extraction of hot-carrier energy. Nat. Commun. 5, 1–5 (2014). https://doi.org/10.1038/ncomms5665

18. ‌Ross, R. T. & Nozik, A. J. Efficiency of hot‐carrier solar energy converters. J. Appl. Phys. 53, 1–7 (1982). https://doi.org/10.1063/1.331124

19. ‌Conibeer, G. et al. Progress on hot carrier cells. Sol. Energy Mater. Sol. Cells 93, 713–719 (2009). https://doi.org/10.1016/j.solmat.2008.09.034

20. ‌König, D. et al. Hot carrier solar cells: Principles, materials and design. Phys. E: Low-Dimens. Syst. Nanostructures 42, 2862–2866 (2010). https://doi.org/10.1016/j.physe.2009.12.032

21. ‌Tesser, L., Whitney, R. S. & Splettstoesser, J. Thermodynamic performance of hot-carrier solar cells: A quantum transport model. Phys. Rev. Appl. 19, 044038 (2023).https://doi.org/10.1103/PhysRevApplied.19.044038

22. ‌Zhang, Y., Conibeer, G., Liu, Sh., Zhang J. & Guillemoles, J.‐F. Review of the mechanisms for the phonon bottleneck effect in III– V semiconductors and their application for efficient hot carrier solar cells. Prog. Photovolt. 30, 581–596 (2022). https://doi.org/10.1002/pip.3557

23. ‌Zhang, Y., Conibeer, G., Zhang, J. & Xiang, W. Study the mechanisms of phonon bottleneck effect in CdSe/CdS core/shell quantum dots and nanoplatelets and their application for hot carrier multi-junction solar cells. Nanoscale Adv. 5, 5594–5600 (2023). https://doi.org/10.1039/d3na00557g

24. ‌Austin, R. et al. Hot carrier extraction from 2D semiconductor photoelectrodes. Proc. Natl. Acad. Sci. USA 120, e2220333120(2023). https://doi.org/10.1073/pnas.2220333120

25. ‌Ašmontas, S. et al. CO2 laser induced hot carrier photoeffect in HgCdTe. Mater. Sci. Forum 384–385, 147–150 (2002).https://doi.org/10.4028/www.scientific.net/MSF.384-385.147

26. ‌Ašmontas, S., Gradauskas, J., Naudjyus, K. & Širmulis, E. Photoresponse of InSb-based p-n structures during illumination by a CO2 laser. J. Semicond. 28, 1089 (1994).

27. ‌Ašmontas, S. et al. Hot carrier impact on photovoltage formation in solar cells. Appl. Phys. Lett. 113, 071103 (2018). https://doi.org/10.1063/1.5043155

28. ‌Shiteng, W. et al. Hot-carrier infrared detection in PbS with ultrafast and highly sensitive responses. Appl. Phys. Lett. 120, 042101 (2022). https://doi.org/10.1063/5.0078394

29. ‌Gradauskas, J. et al. Influence of hot carrier and thermal components on photovoltage formation across the p–n junction. Appl. Sci. 10, 7483 (2020). https://doi.org/10.3390/app10217483

30. ‌Marmur, I. Ya. & Oksman, O. Effect of 10.6 μm laser radiation on the current of a forward biased photodiode. J. Semicond. 11, 2121– 2124 (1975). [in Russian].

31. ‌Bristow, A. D., Rotenberg, N. & van Driel, H. M. Two-photon absorption and Kerr coefficients of silicon for 850–2200 nm. Appl. Phys. Lett. 90, 191104 (2007).https://doi.org/10.1063/1.2737359

32. ‌Schaffner, J. S. & Shea, R. F. The Variation of the Forward Characteristics of Junction Diodes with Temperature. in Int. IEEE Conf. of the Institute of Radio Engineers (IRE) vol. 43 (IEEE, 1955).

33. ‌Green, M. A., Emery, K. & Blakers, A. W. Silicon solar cells with reduced temperature sensitivity. Electron. Lett. 18, 97–98 (1982). https://doi.org/10.1049/el:19820066

34. ‌Zhao, J., Wang, A., Robinson, S. J. & Green M. A. Reduced temperature coefficients for recent high-performance silicon solar cells. Prog. Photovolt. 2, 221–225 (1994). https://doi.org/10.1002/pip.4670020305

35. ‌Cotfas, D. T., Cotfas, P. A. & Machidon, O. M. Study of temperature coefficients for parameters of photovoltaic cells. Int. J. Photoenergy 2018, 59456022 (2018). https://doi.org/10.1155/2018/5945602

36. ‌Sato, S. A., Shinohara, Y., Otobe, T. & K. Yabana. Dielectric response of laser-excited silicon at finiteelectron temperature. Phys. Rev. B 90, 174303 (2014).https://doi.org/10.1103/PhysRevB.90.174303

37. ‌Pelouch, W. S. et al. Comparison of hot-carrier relaxation in quantum wells and bulk GaAs at high carrier densities. Phys. Rev. B 45, 1450–1453 (1992).https://doi.org/10.1103/physrevb.45.1450